

Users often need to pull out the center of a target's coordinate and pass that to manufacturing equipment. For purposes of distortion correction one has to collect a number of targets and their centers
Identifying a target's center can be difficult if it is drawn in a way where there is no vertex or edge intersection to snap to. This is very common when the GDSII data is generated for IC packages or other non-chip layouts.
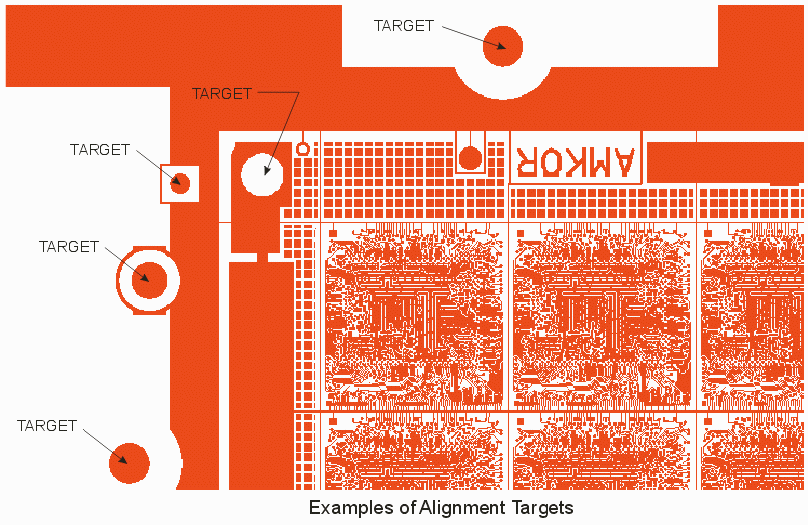
To address this we've created the target acquisition plug-in. While we built this for a distortion correction application it is useful wherever one needs to acquire coordinates of target objects.
This mode snaps to the nearest boundary or path vertex. It is useful when a vertex is located at the center of your target.
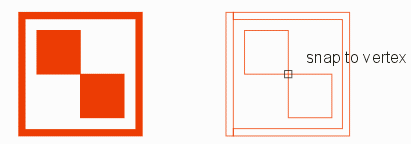
Snap-to-Centroid
This mode first performs a boolean to build a "boundary" around the selected cursor point. Once it builds the boundary it finds the centroid of that boundary. This enables it to find centers for a large range of shapes used in targets.

How Snap to Centroid Works
Since the centroid of our target can contain "edges" from more than one boundary or path the algorithm first performs a union operation on all the polygons within a specified distance of the selection point.
Once that is complete the plug-in can then identify the edges that form a closed loop around the selected point. The centroid calculation is made and the center coordinate is returned.
Because the centroid snap must do a complex boolean computation and then find the surrounding boundary, the user should be zoomed in so that a reasonable number of polygons are in the field of view.
If after clicking Pick Point (in centroid mode) there is a long delay it is normally due to the field of view being too large.
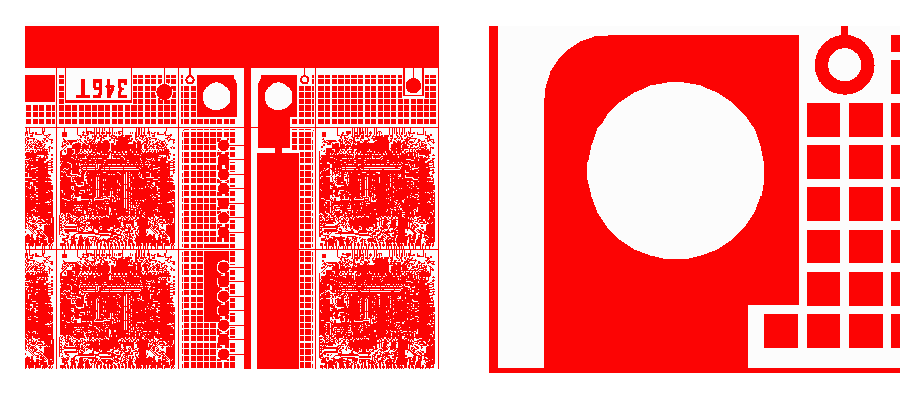
left - field of view is too large. right - field of view is just right to quickly find the centroid.
Can't Find Centroid of Certain Targets
There are certain targets that are "connected" into the rest of the ground or power plane (generally for purposes of plating) that don't form small tight boundaries. In this case, though the eye can detect the center, the algorithm does not.
